Earlier investments make large-scale emission reductions easier to do over time because their unit costs drop
Everyone recognizes that the costs of automobiles, washers, jet planes, and hundreds of other products usually drop with mass production. Most products get cheaper when they stream out of workplaces not by the dozens, but by the tens of thousands, or even millions.
Oddly, however, this basic point – the critical role scale and investments (typically, if imprecisely, known among economists as “induced innovation”) play in pushing down costs of production – is rarely incorporated in earlier generations of climate models.
The ‘canonical’ DICE model pioneered by William Nordhaus and used globally in economics classes, for example, evades this reality. The approach embodies comparisons of simplified worlds with a focus on the optimal trade-off between the presumed cost of emissions reductions today, and assumed by the modeler to fall over time, against the benefit of less drastic climate change in the future. In economic terms, it compares equilibrium conditions in sequential periods.
In this framework, the main research goal is to enumerate the impacts, which then determine the ‘social cost of carbon’ – the damages. To many economists, this defines both the scale of the problem and the solution, in terms of a carbon price to be borne. Generally, the ‘optimal global carbon price’ starts relatively modest and rises over time, often quite sharply. Economic attention thus turns to how best to impose this ‘externality’ cost in markets, and how to deter ‘free riding’ by those who don’t pay.
The focus on comparing well-articulated states of present and future worlds leaves key questions of how transitions happen largely in darkness. Ignoring issues of scale also brings with it a blindness to the inertia that is the flip side of big, complex, and evolving systems. Major energy developments typically involve long-lived capital-specific investments in production, conversion (e.g., power plants, refineries), networks (like electricity grids and fuel distribution), or indeed end-uses (e.g. energy efficiency of buildings). Along with the time required for new energy technologies to diffuse, the result is that these systems are what economists call “path dependent” to an extraordinary degree. What we have today depends on past decisions, what we do today affects what is possible in the future.
The neglect of such issues carries both good news and bad news for efforts to contain climate change. First, the bad news: because the inertial properties of systems are at best partially acknowledged, there is a tendency to underestimate the levels of investment required over time to bring about real change. Inertia means we have to make more effort now to change course, particularly if we are to avoid the most risky climate outcomes at a reasonable cost over time.
But there is also good news: Recognizing how costs can drop as investments are scaled up dramatically transforms assessments of costs in the longer run. Put simply, earlier investments make large-scale emission reductions easier to do over time because their unit costs drop. The fact that most technological systems do respond in this way is not only common sense, but is empirically confirmed by a wide variety of evidence, including studies of patents, private R&D, and technology cost reductions.
Empirical studies also show how energy efficiency accelerates and becomes embodied in capital stock, in response to energy price increases. Indeed, international comparisons of responses to energy price shocks find that countries that sustained higher prices, along with other actions to enhance energy efficiency, have over time become more efficient to the extent that their overall energy bill is no higher (and sometimes is less) than countries that ‘protected’ consumers through subsidies and eschewed energy taxes as discussed in our earlier INET-supported paper on long term energy expenditures.
Our latest INET-funded paper explores how including such dynamics factor into stylized models and changes results. A first conclusion that emerges is that changing course and overcoming inertia requires an effort that grows with the speed of change relative to a ‘characteristic transition timescale’ of the system. The model cannot simply defer action and then cut emissions faster later.
Second, the model represents the overall ability of technologies and systems to respond to economic incentives, scale, and constraints in terms of an aggregate pliability of the system. Implicitly this includes, in particular the potential for investment in low-carbon technologies to drive improvements that at scale make them as cheap as fossil fuels — something observed in recent years in the power sector and increasingly with electric vehicles. Pliability captures the possibility that many of the costs of the initial deployment of cleaner technologies and related infrastructure are in fact transitional investments that reduce subsequent costs.
Our paper shows how these factors can be incorporated in a stylized model – deliberately stripped down to focus on the core implications of inertia and induced innovation for optimal system-level responses in a global cost-benefit setting. We derive an analytic solution (‘Theorem 1’), which pinpoints the mathematical significance of these dynamic factors - and which also highlights analytically the extreme sensitivity of optimal investment to time-discounting in results based on the traditional ‘static’ approach.[1]
An extension of the analysis (‘Theorem 2’) extends this to derive the optimal level of investment when faced with a fixed goal, like the Paris Agreement temperature targets, designed to avoid potentially catastrophic risk thresholds. Whilst conventional economic models tend to ‘optimize’ a trajectory that involves late, steeply ‘negative emissions’ as the temperature limit is approached to help clean up earlier emissions that remain in the atmosphere, the dynamic model shows a much smoother pathway of global emission reductions with more effort to change course immediately.
The bottom line is that our new model demonstrates the optimal global level of low-carbon investment to be bigger – maybe much bigger - when the dynamics of energy systems are incorporated, for the same underlying assumptions about the severity of climate change damages.
This is illustrated in Figure 1, which shows the implications (in the cost-benefit case) of different degrees of pliability in the range 0 to 1. The default DICE case is represented by p=0, i.e., with no inertia and no component of transitional investment associated with lower enduring abatement costs. Its alternate assumption is that low-carbon technologies just ‘get cheaper’ over time, whilst climate damages accumulate. In this case, as a result, the optimum expenditure starts small and rises steadily, reflecting the assumed changing balance of cost-benefit over decades. Global abatement expenditure finally peaks, close to 5% of GDP (ten times the initial level), as emissions finally reach zero early in the next century.
Figure 1: How the trajectory of optimal abatement expenditure (cost-benefit case) depends on the pliability of the emitting system
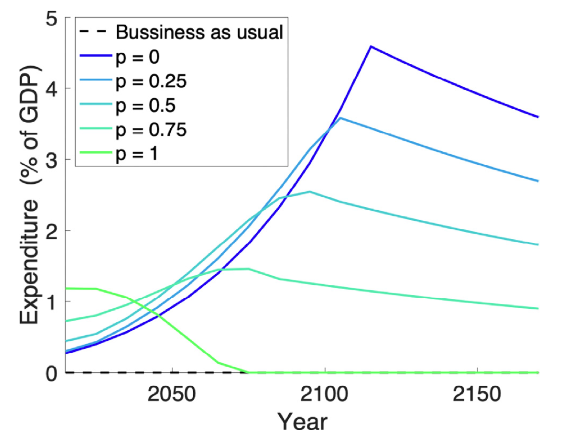
Note: The Figure illustrates the optimal level of expenditure on emissions abatement over 150 years for different cases (all with the same assumed scale of climate damages), as % of GDP. The standard DICE model assumes zero pliability (p=0); whilst the cost of abatement is assumed to fall over time, the expenditure rises steadily, peaking at more than ten times the initial level shortly after 2100. Introducing inertia, coupled with non-zero pliability to reflect induced innovation and path-dependence, systematically increases the optimal initial expenditure and reduces peak expenditure. With a fully pliable system (p =1), the initial optimal expenditure is several times that in the standard case (p=1), at a level which is maintained for 2-3 decades before dropping as the system adjusts towards net zero emission levels.
Our stylized incorporation of dynamic factors points to strikingly different possibilities. Figure 1 illustrates that if the system is semi-pliable (p=0.5), abatement expenditure peaks at about half the time, and at half the level, compared to the classical case (p=0). If the system is fully pliable (p=1) – so that all the costs are in fact adjustment costs – the initial expenditure is much higher, at over 1% of GDP, and remains at about that level for a couple of decades before declining towards a ‘new normal’ of a decarbonized economy, after about 50 years, with stabilized atmospheric CO2.
Despite the stylized inclusion of these dynamic factors, the analytic model is highly simplified compared to the general equilibrium scope of DICE. However, it turns out that all the added complexity of the general equilibrium growth model of DICE makes almost no difference to the results. This is demonstrated by the comparison in Figure 2, which shows the initial optimal expenditure result from our stylized, sectoral analytic model, compared to results from the DICE model when it is extended to include transitional costs and pliability (“DICE-PACE”).
It turns out that a determining factor is the initially assumed ‘abatement cost curve’. The typical DICE formulation (DICE-2016 with standard parametrization) assumes that abatement is initially costly and secures deep emission reductions by assuming costs fall over time, without any specific investment. The results for initial effort (second, orange columns) only approach alignment with the analytic model results at high levels of pliability, which allows both models to converge on cheap abatement in the future; the initial expenditure is then four times that in the standard DICE (i.e., with no inertia or pliability).
Figure 2: How optimal initial expenditure (cost-benefit case) depends on pliability across different model structure and abatement assumptions
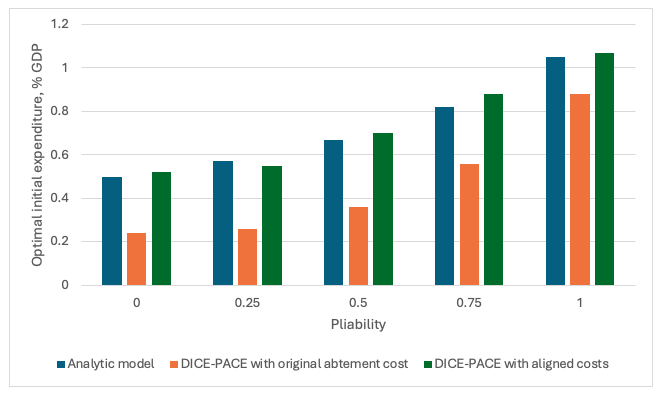
Note: The blue columns show optimal initial global expenditure on abatement from our analytic model, as pliability is increased from 0 (the standard case) to 1. The orange columns show the results from the “DICE-PACE” model (DICE, adjusted to incorporate inertia and pliability) over the range, using the standard parametrization for the abatement cost curve, which starts at much higher level (and hence, much lower abatement and expenditure). When the initial abatement cost curve is aligned (dark green columns), the expanded DICE-PACE model produces almost identical results to that from our far simpler, stylized, partial analytic model.
But when we align the assumed abatement cost curves from the outset, the results align almost precisely, across the full range of pliability. All the apparent sophistication of the GE growth engine in DICE is a distraction. What matters – maybe as much as the damage assumptions – are the assumed level and structure of abatement costs. The general equilibrium components are largely irrelevant compared to the critical, but often unremarked, assumptions about abatement cost structures.
High degrees of pliability may seem implausible to economists used to fixed supply and demand functions – especially given the apparent relative inflexibility (low short-run elasticity) of energy demand. In fact evidence suggests otherwise. Given time, energy systems have proved highly adaptable to energy price shocks. In terms of decarbonization, large-scale investments have resulted in renewables now often being cheaper than fossil fuels for power generation, with similar progress now in electric vehicles. This is equivalent to pliabilities approaching 1, at least for these sectors.
Aside from these global results, there are other subtle implications. The most important is that introducing these dynamics changes the “nature of the game”. It is no longer about distributing a global burden and preventing free riding. Implicitly, it is about investing in the emerging low-carbon economy.
This also means that with induced innovation, climate change is no longer a ‘free-rider’ problem of global burden-sharing, but a competitive game of investment-and-returns. The solutions are not free (at least not initially), but those who invest up-front may gain a leading stake in the solutions which, ultimately, even the most conventional economic models acknowledge will be needed.
And, in the context of highly non-linear climate risks/damages (as represented by an absolute temperature limit; our Theorem 2), those who recognize the importance of inertia will avoid investment in long-lived capital stock, instead switching quickly to low carbon investment. Those who defer action, however, and continue investing in high-carbon infrastructure, bear the risk of facing an overwhelming need to cut emissions rapidly in the future, potentially at very high adjustment costs.
So, incorporating empirically well-established dynamic realities of inertia, induced innovation and path-dependence in models is not some esoteric theoretical exercise. It is an essential need for good economic analysis, with profound implications not only for the scale but also the structure and policy strategies, for optimal responses.
Note
[1] The sensitivity of global climate cost-benefit results to the discount rate is well explored numerically in studies with DICE; our model shows that the optimal investment carries a term that is inversely proportional to the discount rate to the power 6.





